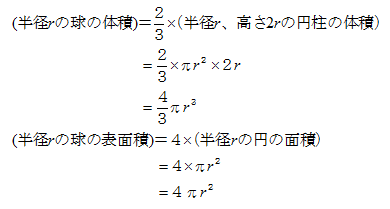
授業実践記録 数学 球の体積 表面積 実験から公式を 啓林館
うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集
数学 球の体積 表面積 公式
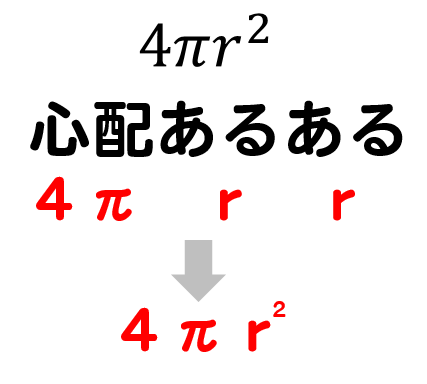
数学 球の体積 表面積 公式-球の体積と表面積 半径 \(r\) の球の体積と表面積を求める公式は以下のようになります。 \(球の体積=\displaystyle \frac{4}{3}\pi r^3\) \(球の表面積=4\pi r^2\) 「なぜこの公式が成立するのか」については中学生の知識の範囲外です。 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、

球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
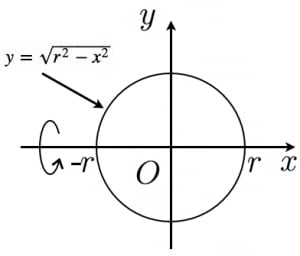
球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 球の表面積公式の証明 (1) この証明は球の表面積を積分によって直接求める方法です。 図のような角度が θ θ から θΔθ θ Δ θ の青い部分の表面積を考える。 この図形を上から見ると円形になっている。 この円形の図形の半径は rcosθ r c o s θ となるV = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin
球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この 三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64( c m 3 ) となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2問題7 (球と円錐の体積) 右の図のような半径9cmの半球があります。この半球と等しい体積の円 すい 錐について考えます。円錐の底面の半径が9cmであるとき,円錐の高さは何cmか求めなさい。
数学 球の体積 表面積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「数学 球の体積 表面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
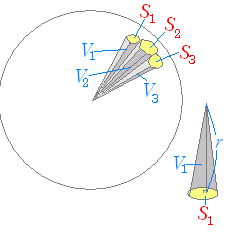
球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ 3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ 中学数学 球の体積の求め なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 ただし は幅 の部分の中央線である。 証明 より, (証明終わり) このような考え方を使って, 直円錐の側面積の一部分を考える。
Incoming Term: 球の体積 表面積 公式, 球の体積 表面積 公式 中学, 球の体積 表面積 公式 なぜ, 数学 球の体積 表面積 公式,




0 件のコメント:
コメントを投稿